Volume of Parallelopiped and Tetrahedron

A parallelopiped is a 3-D object, each of whose faces is a parallelogram.

A rectangular parallelopiped is the one, whose faces are rectangular.

A cube is a rectangular parallelopiped, whose edges are of equal length.

---

A tetrahedron is a 3-D object, whose all faces are triangular. It can be shown that a parallelopiped can be decomposed into 6 tetrahedra.

Image Source : https://www.dune-project.org/

For a visual proof :  1 Parallelopipded  = 6 Tetrahedra

---

 

Let there be 2 such objects, whose coterminus edges are identical. Then, the volume of the tetrahedron is th of that of the parallelopiped. The expression can also be obtained using the following theorem :

Vector Algebra : Theorems (I)

In this blog, we will prove fundamental theorems in vector algebra. These theorems are in accordance with the +2 curriculum.

Theorem 1 : Collinear Vectors

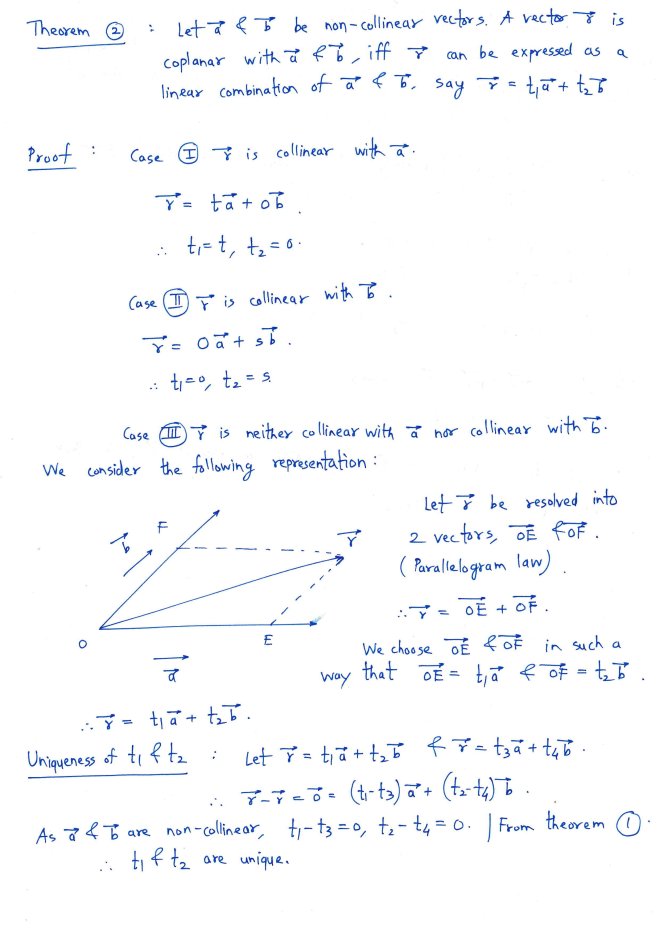
Theorem 2 : Non-collinear and Coplanar Vectors

Theorem 3 : Coplanar Vectors

Theorem 4 : Non-coplanar Vectors